Dzielność morska: współczynnik komfortu jachtu

Lady Moura w Monte Carlo (w 2011r dopiero na 24 miejscu na liście największych jachtów prywatnych) Właściciel: Nasser Al-Rashid
Fot. własna

Czy można zmierzyć coś tak bardzo ulotnego jak komfort jachtu? Jak do tego podejść w projekcie jachtu? Co uwzględnić w budowie łodzi? Jak ocenić pod tym względem jacht, który zamierzamy kupić? Okazuje się, że można spróbować. Nie myślę tutaj o ilości luksusów na m2. Interesują mnie przyspieszenia w ruchu jachtu, zależne od fali.

Wszelkie próby policzenia realnych przyspieszeń poruszającego się jachtu, aczkolwiek możliwe, są mało przydatne, ze względu na słabo dopracowany stochastyczny model falowania morza. Model może i jest niezły, ale morze wciąż nieprzewidywalne. Poza tym obliczenia takie byłyby niezwykle skomplikowane. Trzeba więc poszukać w miarę prostego narzędzia porównawczego. Czesław Marchaj w swojej doskonałej książce "Dzielność morska, zapomniany czynnik" w rozdziale czwartym czwartym publikuje ciekawy wykres uzależniający zdolność do działania załogi od panujących na jednostce przyspieszeń i okresów drgań.



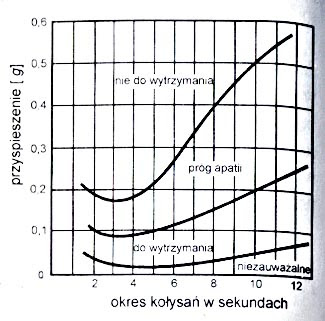Zależność sprawności psychofizycznej załogi w zależności od wielkości przyspieszeń i okresu kołysań. Wykres pochodzi z książki Cz. Marchaja Dzielność morska, zapomniany czynnik



Zadaje to jakby kłam często spotykanym na forach internetowych twierdzeniom, że dzielność morska jachtu  zależy od dzielności załogi.  Nawet tak niskie przeciążenia jak 0,2g przy odpowiednio niskim okresie drgań definiowane są już jako "nie do wytrzymania". Nadmienić należy, że zbyt duże obciążenie wodnicy jachtu też niczemu dobremu nie służy. Nie chcemy przecież aby jacht kołysał się jak "w pijanym widzie". Konieczne staje się wypracowanie optimum.

Próbę określenia współczynnika komfortu jachtu podjął Ted Brewer. Jego wzór ma postać:

Wsp. komfortu wg T. Brewera = wyporność/(.65*(.7*lwl+.3*loa)*szerokość ^1.33)

Wartość tego współczynnika Ted Brewer określa od 5,0 dla superlekkich jachtów do 60 dla super ciężkich jachtów, takich jak Colin Archer kecz. Średnie jachty mają mieć średnio czyli w okolicach 30. Czyli dużo mądrzejsi po analizie tego wzoru nie jesteśmy.

Bardziej przypadło mi więc do gustu podejście Dave'a Gerr'a, który spróbował relację wyporności jachtu do powierzchni wodnicy zbadać na przykładach jachtów powszechnie uznanych za dobre. Dave Gerr opublikował nawet wykres w swojej książce Nature of Boats. Jednak każdorazowe odczytywanie z wykresu i wstawianie do dalszych obliczeń jachtu jest mocno kłopotliwe. Postanowiłem metodę nieco stuningować.

   Postanowiłem pójść tą drogą. Na początku oparłem się na jachtach wybranych przez Dave'a Gerr'a i aproksymowałem jego jachty do podobnej do jego krzywej. Mało powiedziane podobnej, wyszła praktycznie identycznie i to jako funkcja wykładnicza. Czyli zaczynamy być w domu, jeśli chodzi o metodę matematyczną. Jednak ja jestem małej wiary i podpiąłem wybrane przez siebie jachty, o których wiem, że są powszechnie uważane za dobre. Po aproksymacji do krzywej, wzór z mojego zestawu jachtów pokrył się praktycznie w 100% z Krzywą Dave'a Gerr'a. Przyjąłem to za wystarczający dowód na słuszność takiej krzywej.

Mój wzór  na modelową pod względem komfortu wyporność jachtu wygląda tak:

Wyporność komfortowa jachtu=0,09*pow wodnicy^1.459

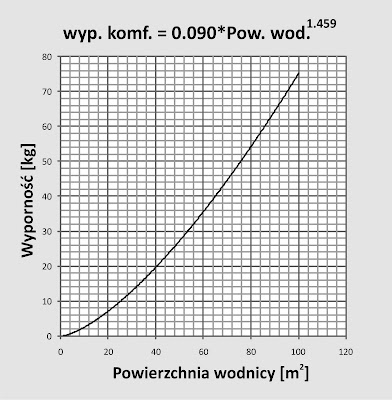Krzywa zależności między powierzchnią wodnicy konstrukcyjnej a optymalną wypornością jachtu



No ok ale skąd wziąć na szybko powierzchnię wodnicy jachtu. Problem jest zasadniczo prostszy do rozwiązania niż mogłoby się wydawać. W dobrze zaprojektowanym kadłubie wypornościowym jest to 68% z iloczynu długości wodnicy * szerokość wodnicy. Wahania wskaźnika 68% są tak niewielkie, że leżą w granicach błędu całego rozważania. W kadłubach ślizgowych ta wartość jest delikatnie większa, ale zazwyczaj nie przekracza 80%. Kadłuby ślizgowe z definicji będą lżejsze niż kadłuby jachtów wypornościowych. Przy badaniu komfortu jachtu ślizgowego po prostu sprawdzamy jak daleko uciekliśmy od statystycznego optimum.

Pragnę zwrócić uwagę, że rozważania Ted'a Brewera określają wartość wyimaginowanego bądź co bądź współczynnika. W naszym wzorze otrzymujemy "receptę" na modelo porządaną wyporność.

Wzór był wyznaczony ze zbioru 100 jachtów o wyporności od 3 ton w górę. To co się dzieje poniżej 3 ton jest raczej hipotetyczne i wynika z charakteru krzywej, jednak w każdej chwili bazę danych do aproksymacji krzywej można rozszerzyć, albo całkowicie zmienić do indywidualnego zbioru odpowiadającemu naszej wizji optymalnego pod względem komfortu jachtu.

Zwiększając szerokość jachtu przy stałej długości zmniejszamy obciążenie jednostkowe wodnicy konstrukcyjnej. Słowem modelowa wyporność komfortowa będzie większa niż nasza z poszerzonym kadłubem, co doprowadza do wniosku, że jachty nakierowane na osiągi z definicji muszą dość twardo poruszać się po fali. Szczególnie jest to odczuwalne w szybkich jachtach ślizgowych.

Wzór ten ma dość fajne zastosowanie podczas projektowania wstępnego jachtu. Zakładamy rządany stosunek Delta/KLW. (kalkulator znajdziecie tutaj Kalkulator delta/L ratio) Mając założoną długość, wyporność, ze wzoru na komfort natychmiast otrzymujemy optymalną szerokość. jeśli przy okazji nasze rozważania są zgodne z optimami dla oporów, to jesteśmy w domu. Jeśli zwiększamy szerokość wypłycając kadłub, wciąż mamy kontrolę jak bardzo "przeginamy". Zresztą zastosowań tego wzoru znalazłem jeszcze kilka. Okazał się wyjątkowo przydatny.

Niebawem na blogu zamieszczę stosowny kalkulator liczący optymalną komfortową wyporność. 8JCTV8SKS9KK